Kalendarium part 1

A hundred years at one's fingertips

Nov 25, 2024

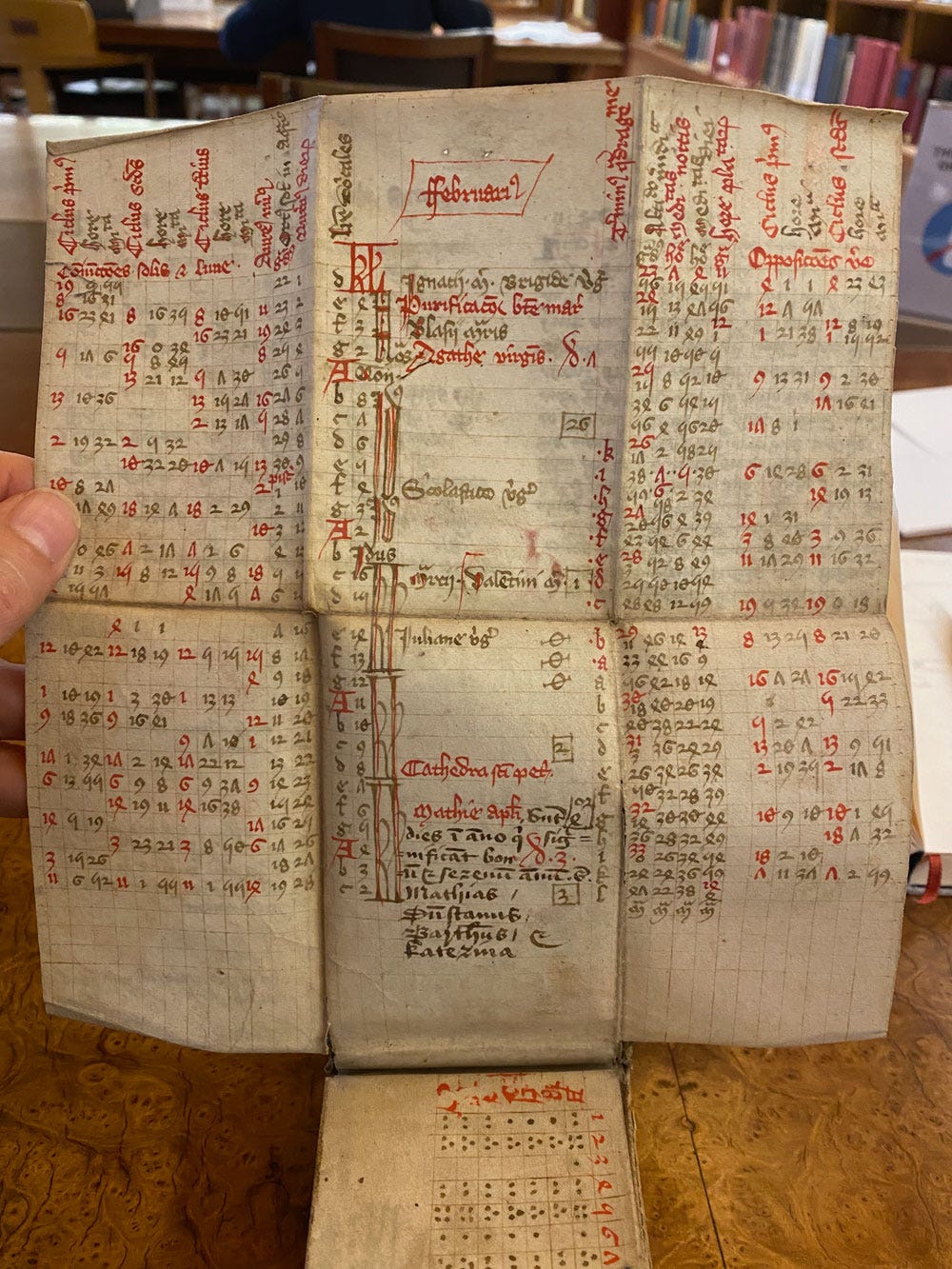
When I started my research on medieval timekeeping at the Bodleian, the very first manuscript I found myself examining was an intriguing, minute, folded affair.

I soon found out it was generally referred to as a folded almanac (designed to hang from the belt and be consulted in that position), and furthermore that the calendar it contained, with additional tables that were bewildering to me at the time, wasn’t a one-off. This was a copy of John Somer’s Kalendarium, which was “a thing” in the late fourteenth and fifteenth centuries.

This kalendarium or kalendar, to differentiate it from our modern conception of calendars, is basically what we would call today an almanac in that it contains a lot of additional information such as eclipses, planetary hours, and the relationship of the Zodiac with the body. The John Somer kalendar follows a particular structure that has been copied (and sometimes adapted) in countless books and portable almanacs of the period. The point of this post, which I had to break down into two parts, is to go through the purpose of each component of the kalendar, and how to use it – as well as sharing images of this extraordinary work that is often copied in the most exquisitely tiny hand. In this endeavour I’m heavily indebted to The Kalendarium of John Somer, edited by Linne R. Mooney1. I have mostly digested and reworded her methodical primer, and provided images from various manuscripts I looked at to illustrate it directly.

So who was John Somer? Friar Johannes Somer (ca. 1340-1410) was a Franciscan monk, contemporary of Chaucer, who came to Oxford to study astronomy and established a reputation for himself as an astronomer. He wrote his kalendar ad meridiem Oxonie (“for the meridian of Oxford”) in 13802, and updated the charts through the 90’s. Mooney writes:

Only at Oxford would Somer have had access to the learning of the Merton school of astronomy: its masters, its books, its equipment. Merton had been founded in 1264 for the education of the secular clergy, and had already in its first century acquired a reputation for the study of the natural sciences, and especially of astronomy.

It’s a wild coincidence, or serendipity, that I should have been at Merton myself, 644 years later, when undertaking this research! Below, I will elucidate the different sections of the Kalendarium in order. Photos are mine, and shelfmarks are given.

1. Table for Reading Hindu-Arabic Numerals

At the time Somer was composing his kalendarium, the Hindu-Arabic numerals were not well-known in Europe3. But they could do what Roman numerals were simply incapable of: fit easily into the tiny spaces of the numerous, close-set tables that were indispensable for such a tool. Therefore Somer, like many others, chose to go with this unfamiliar system, and to include this Tabula Docens Algorismum Legere to clarify how to read it. Originally he only provided a guide for numbers up to 60, the highest number required in a kalendarium, but later copyists of his system often adapted it for their own use or time: in the example above, the guide goes up to 10,000. But in many copies, this table was left out altogether, presumably because Hindu-Arabic numbers were now too widespread for it to be needed4.

2. Leap Year Table

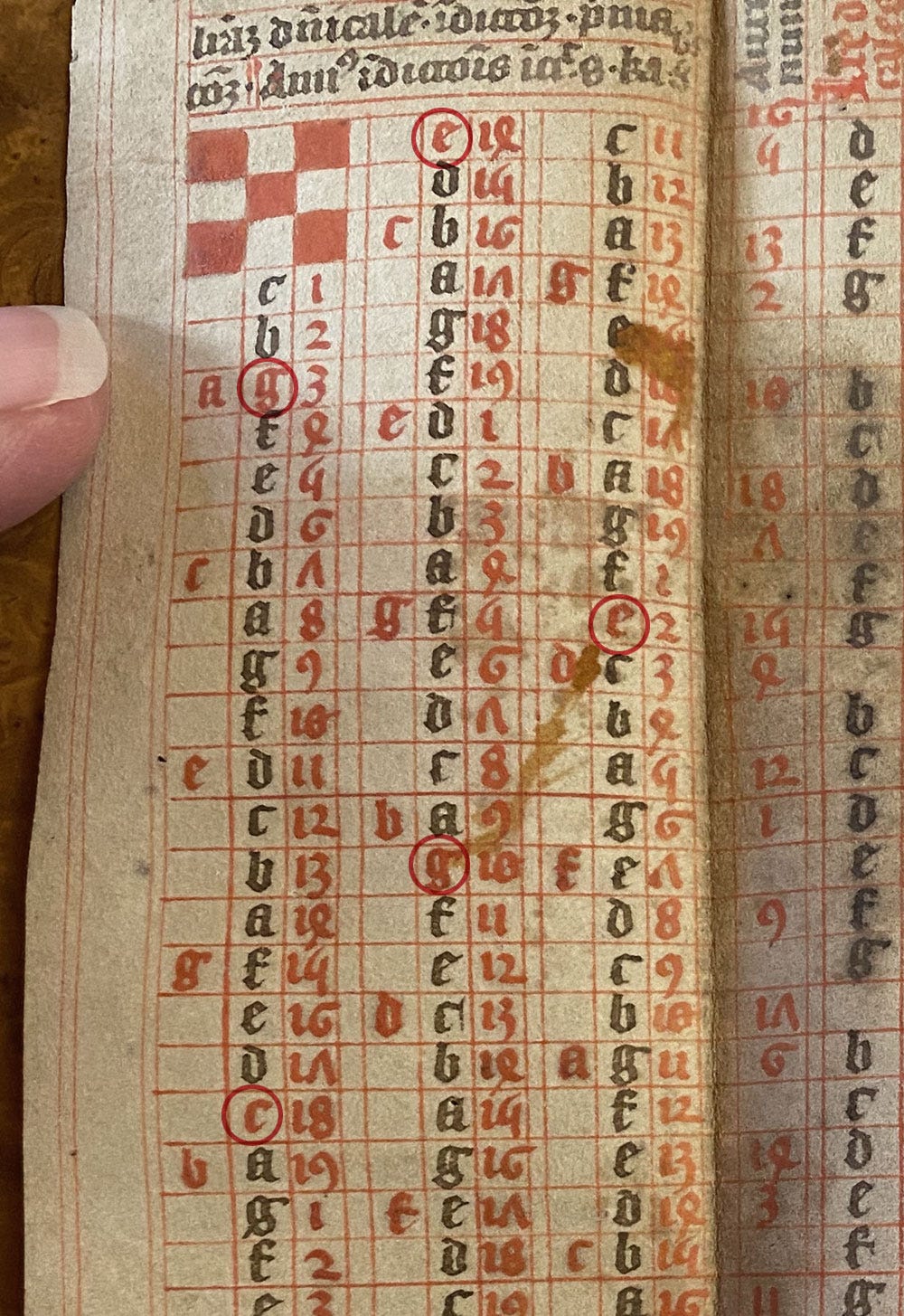
The Tabula Bisextilis is the key to the whole kalendarium, allowing it to be used for many years. It provides three pieces of information for each of the years listed: the Dominical Letter, indiction, and Golden (or Prime) Number. Let’s take these one by one, using the example that occupies the left third of both spreads above.

The Dominical Letter (DL):

You can probably tell that’s the Sunday letter (Littera dominicalis), but what exactly does that mean? Every year, the 1st of January is assigned the letter A. January 2nd was B, 3rd was C and so on till the 7th (G), then the cycle of seven letters repeats until the end of the year. The letter that falls on a Sunday that year, is the DL for that whole year. In 2024, January 1st (or A) was, conveniently, a Monday, so G was the DL for 2024. You could leaf through the entire kalendar and every single G would signal a Sunday. But in 2025, the first Sunday falls on January 5, and the DL will therefore be E: you can leaf again through the same kalendar next year, knowing Sundays are now indicated by E. A new almanac needn’t be laboriously copied, in fact if you count the rows on the table, above, you’ll see this one is valid for 84 years. The column I highlighted below notes the DL for each of these years. And you may notice that on the left, every fourth year, there is an extra DL, marked in red. Here’s why…

A bissextile or leap year is one in which an extra day is added in order to compensate for the fact a solar year5 is not really 365 days, but in truth 365.25 days, producing one whole bonus day every four years. This quickly adds up so that the calendar gets out of sync with the seasons and holidays, so this simple solution redresses the situation regularly enough for it not to be disruptive. Nowadays February is 29 days long in a leap year, when it’s usually 28 days. In Medieval times however, during leap years February 24 is simply doubled – it lasts two days.

The effect on the arrangement we just learned is that up till February 24, the DL is as I explained, but after that date, during a leap year, the cycle of letters is pushed out of sync. This is why two DLs are given on those years: the red one on the left is for the first two months(ish) of the year, the one in black in the column is for the rest. Whew!

The indiction:

This is a dating cycle of 15 years, that was used in the Roman Empire6. By Somer’s time it’s rarely used, but it can still be found in early versions of his kalendar. The indiction for the first year is found to the left of the DL column, circled red below. After that, in a cycle of 15, every first indiction year is noted by writing the DL in red.

Except this particular scribe seems to have forgotten all about the inception cycle after the first red letter, so here’s a more complete table from our second example (which on the other hand is missing the indication of the first year).

The Golden Number (GN):

To the right of the DL column we can see a sequence of numbers that run to 19 and start again. This is another cycle: the Metonic cycle7, which is essential for calculating Moon phases in respect to the Sun. The Moon’s cycle is in no way synchronised with the Sun’s: a solar year is somewhere between 12 and 13 lunar months. Meton worked out that 19 solar years are effectively the same duration as 235 lunar months: every 19 years, a given day of a lunar month occurs on the same day of the solar year.8 For instance, there will be a new moon on December 1st 2024; thanks to the Metonic cycle I can say that there was also a new moon on December 1st 2005, 19 years ago.

The Golden or Prime number (Aureus numerus) is simply the place of any given year in the Metonic cycle, and the one for the first year is given at the top, to the right of the DL (circled in gold below). This is important to locate the full moons in any given year, in order to know the date of Easter among other things. How this number is obtained is by a simple calculation: divide the year by 19, take the remainder and add 1. For instance, 2024 divided by 19 is 106, remains 10. 10+1= 11, the Golden Number for 2024.

3. Table of Moveable Feasts:

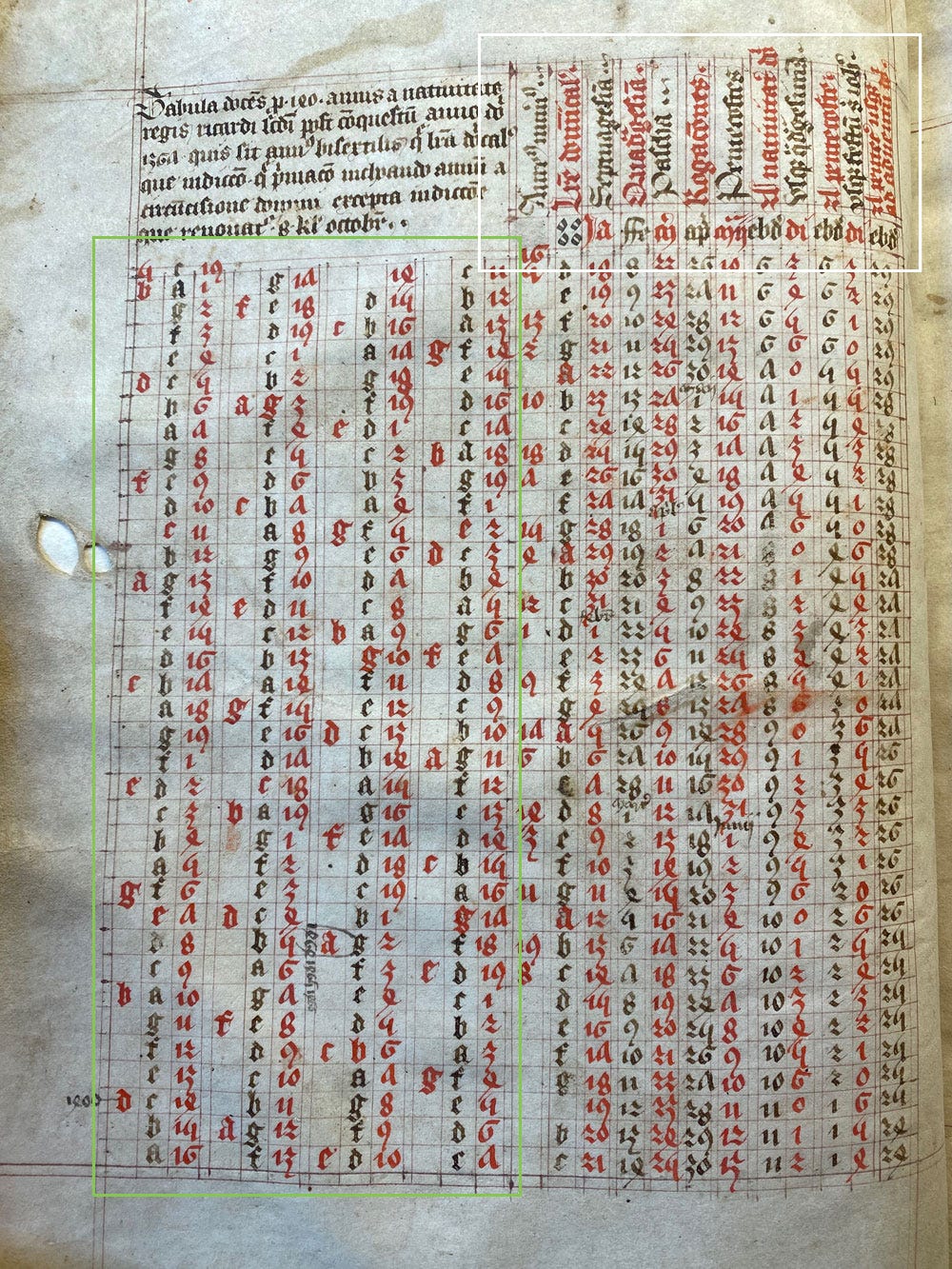
The Tabula Festorum Mobilium (aka Easter Table) closely follows the Leap Year Table, as seen on this large sheet; in our earlier examples it occupies the remaining two thirds of the spread. Above, the part framed in green is the Leap Year Table we just studied. To explain the contents of the Easter Table, let’s focus on the white frame and rotate it 90° to make out the column titles:

Aureus Numerus: The Golden Number obtained from the Leap Year Table. The first year is 16, above the line, and the rest of the column may strike as odd because it’s no longer in sequence. But this is because the days of the months, in the Jan to May columns, are in sequence, and both the GN and DL (next column) are redistributed accordingly.
Littera Dominicalis: The Dominical Letter, also obtained from the Leap Year Table. I’ll explain below how these two are used in this table.
Septuagesima: The 9th Sunday before Easter. The secondary header indicates the dates underneath are in January, at least to begin with; at some point down the column the month switches to the next, as seen in these two close-ups.

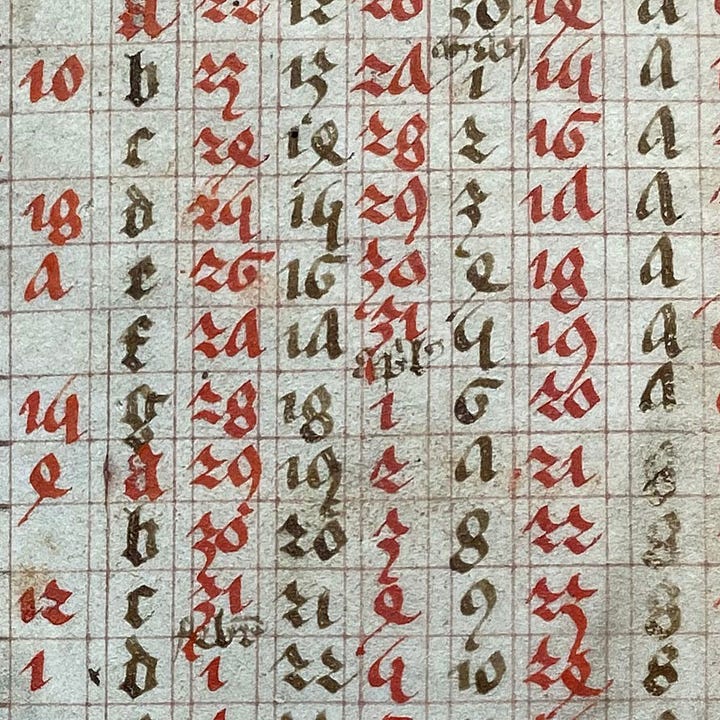
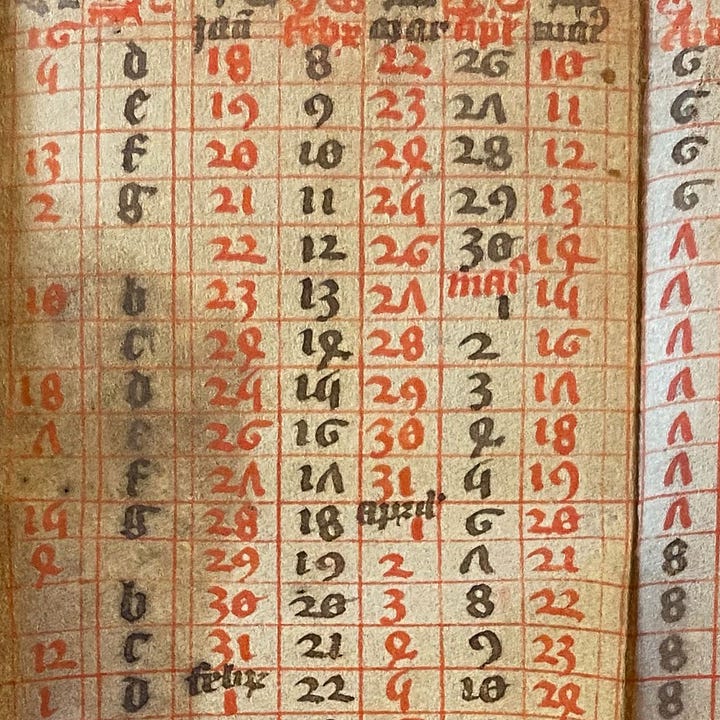
Quadragesima: The first Sunday in Lent, after Ash Wednesday, which occurs in February or March.
Easter (Pascha): This important Christian holiday is observed on the first Sunday after the first full moon on/after the spring equinox.9
Rogaciones: Rogation Sunday, the Sunday preceding the Ascension.
Pentecost: or Whitsunday, in May or June.
Next is a double column showing the number of weeks (ebdo) and days (di) from Christmas to Quadragesima.
Another double column showing weeks and days from Pentecost to the birth of John the Baptist.
Finally, the number of weeks from Pentecost to Advent, which is the fourth Sunday before Christmas.

How to use the Table of Moveable Feasts, step by step:

Locate or calculate the GN for the target year. Let’s take the year 1380, whose GN is 1310.
Look up the corresponding DL in the Leap Year Table. For 1380, being a leap year, it would be A before Feb 24 and G after. Easter can’t possibly occur before Feb 24, so for that feast and those that follow it, only G concerns us.
In the Table of Moveable Feast, we find 13 in the GN column and the first instance of G below it in the DL column. This is the row that gives the dates for all the feasts of that year. Easter in particular was on Sunday March 25 in 1380.

This is probably enough to digest in one go, so I’ll end here and will pick up soon from section 4: The month-by-month calendar.

Leave a comment

Somer, John. The Kalendarium of John Somer. Ed. by Linne R. Mooney. Athens: University of Georgia Press, 1998. Print.

This was ordered by his superior Thomas Kingsbury, at the request of Joan of Kent (Princess of Wales and mother of Richard II). Note that 6 years later a similar Kalendarium was composed by Nicholas of Lynn, a Carmelite friar who was also an Oxford astronomer, at the request of JOhn of Gaunt, Duke of Lancaster. Both versions, which don’t differ greatly, integrated astronomical data in a unique new way and both were extremely popular, so that their respective parts are sometimes mingled. I’m focusing strictly on Somer’s as the material is already complex enough.

I’ve written about their history at length in my book Story of Abjad, but let me just say here that it took another century for them to become familiar even to the general public. Meanwhile, they were used alongside the long-standing Roman numerals.

As a matter of fact this was the only example of this table I could find among the fifteen-odd kalendarii I examined.

This is also known as tropical or astronomical year, defined as the time the Sun takes to return to the exact same place in the sky as viewed from the Earth (obviously it’s the Earth which orbits, but this is how it looks). But seen from a fixed point in space, the Earth completes its orbit in 1 sidereal year, which is 366.24 days long. Natural time is so much more complicated than we’re taught and I’m not even scratching the surface.

More detail, from Wikipedia: “An indiction (Latin: indictio, impost) was a periodic reassessment of taxation in the Roman Empire which took place every fifteen years. In Late Antiquity, this 15-year cycle began to be used to date documents and it continued to be used for this purpose in Medieval Europe,and can also refer to an individual year in the cycle; for example, "the fourth indiction" came to mean the fourth year of the current indiction. Since the cycles themselves were not numbered, other information is needed to identify the specific year.”

Named after Meton of Athens who calculated it in the 5th century BC. If you prefer, it’s also known as enneadecaeteris...

A more accurate cycles of 76 years (Callippic cycle) was later calculated, but the shorter Metonic cycle was more practical and was functional enough, so it endured.

In Somer’s time this was according to the Julian calendar. Nowadays, to draw a very rough picture, Western churches use the Gregorian calendar while Eastern churches adhere to the Julian one for liturgical purposes, which is why two separate Easters are celebrated now, at least in places (like my native Lebanon) where both are officially observed.

I’m using Mooney’s own example because a leap year is a good illustration and because using 2024 wouldn’t work well, as the calendar has been reformed and days have shifted since the Middle Ages.